FREE document explaining Density and Pressure.

Air density is defined as the mass of air per unit volume. It is a measure of the number of air molecules in a unit volume of air. Air is held to the earth’s surface by the force of gravity and so, the higher one goes in the atmosphere, the ‘thinner’ (less dense) the air. An International Standard Atmosphere (ISA) has been defined as a measuring stick against which the actual atmosphere existing at a particular time and place can be compared. A number of characteristics (such as pressure, temperature and density) are specified for various levels in the International Standard Atmosphere.

• Air pressure in the ISA is 1013 hectoPascals at Mean Sea Level and the pressure decreases with altitude, at about 1 hPa per 30 feet gain in height in the lower levels of the atmosphere.
• Air temperature in the ISA is +15^oC at Mean Sea Level and decreases at approximately 2oC per 1000 feet gain in altitude.
• Air density in the ISA decreases with a gain in altitude.

The main function of the Standard Atmosphere is to calibrate altimeters (which are basically pressure reading devices) so that they match up certain air pressures with the correct altitudes. With the altimeter set on 1013 hPa (ISA MSL), an altimeter will display a height that corresponds to an altitude in the International Standard Atmosphere. This is known as Pressure Height.

Fig 1. With standard pressure 1013 set in the sub-scale window an altimeter reads pressure height

Actual Mean Sea Level Pressure Varies

The actual air pressure that exists at a given place varies from day to day and from hour to hour. In aviation, we cope with this by using the QNH pressure setting in the altimeter sub-scale that relates the altimeter reading to the sea level pressure, whatever it happens to be at that time and place.

For the altimeter to read altitude (height above sea level) accurately, you must ensure that the correct QNH is set in the sub-scale.

Calculating pressure height, knowing altitude

We can determine pressure height by either: reading the altimeter with 1013 set in the sub-scale; or by using the difference between QNH and 1013 to convert altitude to pressure height. If actual sea level pressure differs from the standard atmosphere of 1013 hPa, then a simple diagram will help us with any calculations of pressure height. We convert altitude to pressure height by allowing 30 feet for each 1 hPa pressure difference.

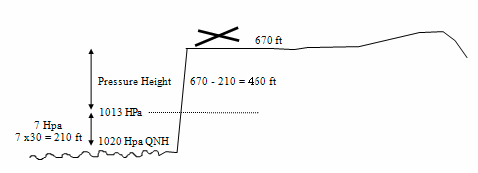
EXAMPLE 1. An aerodrome of elevation 670 ft has an Aerodrome QNH of 1020 hPa. What is its pressure height?

Elevation = 670 feet
QNH = 1020 hPa

Answer: Pressure Height =  670 – 7 x 30 = 460 feet

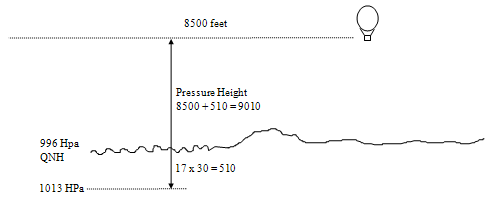
EXAMPLE 2. A balloon is flying at an altitude of 8,500 ft. QNH 996 hPa. What is its pressure height?

Altitude = 8500
QNH = 996 hPa

Answer: Pressure Height = 8500 + 17 x 30 = 9010 feet

Altimetry procedures for cruising aircraft

Cruising below 10,000 ft in Australia, separation from terrain is a consideration and so height AMSL is worthwhile knowing reasonably accurately. To allow the altimeter to indicate altitude (ie height AMSL), it is usual to cruise with QNH set in the sub-scale. QNH varies from time to time and place to place and must be continually updated (every hour or so as advised). Since the highest terrain in Australia is less than 8,000 ft AMSL, cruising aircraft above 10,000 ft have 1013 hPa set in the altimeter sub-scale. This does not have to be continually updated of course. It still provides safety in that all aircraft above 10,000 ft have 1013 hPa set and can determine their vertical separation from each other using pressure heights indicated, rather than altitude. As a matter of convenience, pressure heights above 10,000 ft are referred to as flight levels.

• Pressure height 15,000 ft is FL150
• Pressure height 21,000 ft is FL210

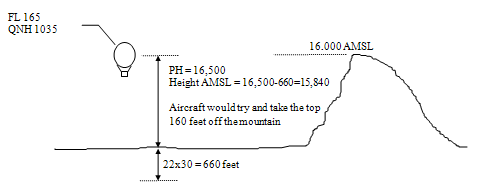
Fig 3. The highest terrain in Papua New Guinea is approximately 16,000 ft AMSL.
For this reason, the transition from QNH setting to 1013 hPa is not made in PNG until 20,000 ft.

Air temperature decreases with height in the standard atmosphere

In the International Standard Atmosphere (ISA) the Mean Sea Level (MSL) temperature is +15^oC and decreases by 2^oC for every 1,000 ft gained in altitude. ISA MSL is another way of saying “pressure height zero”

• At 1,000 ft pressure height, ISA temperature = +15 -2 = + 13^oC
• At 2,000 ft pressure height, ISA temperature = +15 – 2×2 = 11^oC
• At 3,000 ft pressure height, ISA temperature = +15 – 3×2 = +9^oC
• At 7,000 ft pressure height, ISA temperature = +15 – 7×2 = +1^oC
• At 8,000 ft pressure height, ISA temperature = +15 – 8×2 = -1^oC
• At 20,000 ft pressure height, ISA temperature = +15 – 20×2 = -25^oC
• At FL250, ISA temperature = +15 – 25×2 = -35^oC

Any variation from ISA temperature at a given pressure height may be written as either

• the actual temperature, eg. +14^oC at pressure height 3,000 ft; or
• the ISA variation, eg. at PH 3,000 =14^oC = ISA+5

EXAMPLE 3: What temperature is PH 16,000, ISA -10?

At 16,000 ft PH ISA = +15 – 2×16 = +15 – 32 = -17^oC
ISA-10 = -17 – 10 = -27^oC

Answer: Temperature = -27^oC

EXAMPLE 4: Altitude 10,000 ft. QNH 1030 Outside Air Temperature (OAT) – 12^oC

What ISA variation is this?

PH = 10,000 – 17×30 = 10,000 – 510 = 9,490, say 9,500 ft.
At PH 9,500, ISA = +15 – 2 x 9.5 = =15-19 = -4^oC
At PH 9,500, -12^oC, which is 8^oC colder than -4^oC, is therefore:

Answer: ISA Variation = ISA-8

Air Density varies with Height

In the Standard Atmosphere, pressure height and density height at any one point are equal.   As air warms up at constant pressure, it expands. This causes the air density to decrease, since there will be fewer air molecules per unit volume, yet the pressure height will remain unchanged.   For each 1^oC in excess of ISA at a given pressure height, the density height will be approximately 120 ft higher than the pressure height.

Calculating Density Height

EXAMPLE 5: Determine the density height at pressure height 13,000 ft (Flight Level 130) ISA + 10

DH  = PH 13,000 + 10x 120 = 13,000 + 1,200 = 14,200

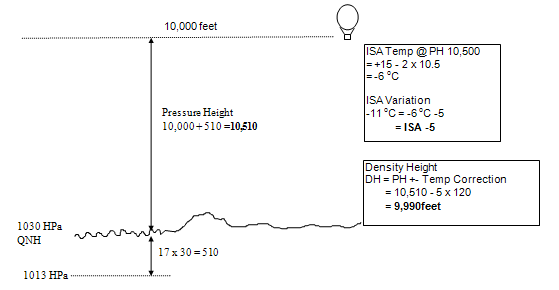
EXAMPLE 6: Determine the density height at altitude 10,000 ft, QNH 1030, +6^oC

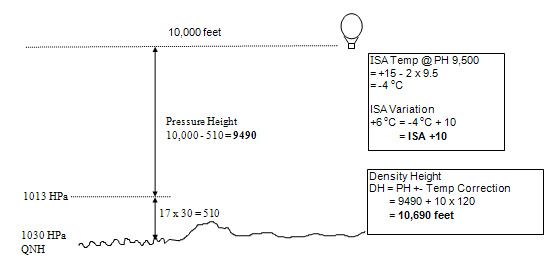
EXAMPLE 7: Determine the density height at altitude 10,000 ft, QNH 996, -11^oC

A pdf version of this page can be downloaded using this ‘how to calculate pressure height and density height‘ link. There are also some practice density height exercises here.

Back to Pilot Exam Help Index

Technical data content credited to Mr Steve Griffin